There Is No True OLL Parity above Three Dimensions
Last modified December 19, 2022.
Introduction
In the speedcubing community, the word “parity” for a given puzzle often refers to “an endgame situation that does not show up on the 3x3x3 that sometimes shows up on that puzzle”. These parity situations often require long algorithms to solve, frustrating speedcubers by slowing down their times.
Another definition of the word “parity” occurs in group theory, where the “parity of a permutation” refers to whether an even or odd number of swaps are required to achieve that permutation. If an odd number of swaps are required, the permutation is an odd permutation. Otherwise, the permutation is an even permutation. Solving a twisty puzzle intuitively often requires knowing this definition of parity.
Even-layered \(n^3\) cubes where \(n \ge 4\), such as the 4x4x4, can experience a situation called Orientation of Last Layer (OLL) parity, where a single pair of edge pieces need to be swapped near the end of the solve (Figure 1). This situation involves parity in both senses of the word. Firstly, OLL parity is an endgame situation that does not show up on the 3x3x3, and only sometimes shows up on the even-layered puzzle. Secondly, the situation involves a single swap, or an odd permutation, of the edge pieces.

Figure 1: OLL parity on a 4x4x4 in Twizzle.
Higher-dimensional cubes can be solved using strategies for three-dimensional cubes, because one can use analogies to translate concepts to higher dimensions. However, it turns out that higher-dimensional even-layered puzzles cannot experience OLL parity in the exact same way as a three-dimensional even-layered puzzle, because they cannot encounter odd permutations of any piece type at all.
3-cycles, even permutations, and odd permutations
Even permutations, such as the 3-cycle, are useful in cubing. A 3-cycle describes any algorithm that cycles three pieces. For example, given three pieces A, B, and C, the cycle A->B->C->A is a 3-cycle. The 3-cycle is an even permutation because it involves an even number of swaps. For example, if one swaps A with B, and then swaps the piece in A’s former position (i.e. B) with C, they achieve the previous cycle A->B->C->A. Figure 2 shows an example of a 3-cycle on the 4x4x4.

Figure 2: A 3-cycle on the 4x4x4 in Twizzle. Three edge pieces have been cycled.
Solving the cube blindfolded often involves solving one or two pieces at a time using 3-cycles. Strategically using 3-cycles can also be a useful strategy for intuitively solving puzzles, because 3-cycles are usually relatively easy to find, and only affect three pieces at once, allowing the solver greater control over the state of the puzzle.
Like addition, two even permutations result in another even permutation, and two odd permutations result in an even permutation. Therefore, odd permutations cannot be attained only through using 3-cycles. In other words, odd permutations can be more “troublesome”, because they disrupt the flow of 3-cycles, and need to be handled separately.
Higher-dimensional parity
It turns out the MC4D message archive has older posts on even and odd permutations on higher-dimensional cubes. In 2006, Don Hatch wrote a thread on a general 2^d and 3^d solver, with a note that for \(d \ge 4\), the \(2^d\) cube cannot have odd permutations. In 2009, a thread on higher-dimensional parity appeared, where at the very end of the thread, David Smith stated some propositions on higher-dimensional parity. I provide proof sketches for some of those propositions below.
Theorem 1: For \(3^n\) cubes where \(n \ge 3\), the 2-coloured (2c) pieces of the puzzle can be in an odd permutation. The 3-coloured (3c) pieces of the puzzle can also be in an odd permutation. The 2c pieces of the puzzle are in an odd permutation if and only if the 3c pieces of the puzzle are in an odd permutation.
Proof sketch: Consider a solved \(3^n\) cube, and a rotation of a single facet of that puzzle by 90 degrees. Such a turn effects a 4-cycle of four 2c pieces, while leaving the other 2c pieces in place. Therefore, a single 4-cycle occurs on the 2c pieces, causing them to be in an odd permutation.
The same turn also effects 4-cycles on 3c pieces on the same facet. Four of those 3c pieces are on the same slice as those 2c pieces, whereas all the other ones fall symmetrically on both sides of the slice. In other words, the 3c pieces not on the same slice as the 2c pieces can be considered in pairs. Therefore, there are several pairs of 4-cycles of 3c pieces, plus a single 4-cycle of 3c pieces, which add up to an odd number of 4-cycles. The 4-cycle is an odd permutation, and an odd number of odd permutations is an odd permutation, so the 3c pieces are also in an odd permutation.
Because every solvable permutation can be broken down into a series of valid facet twists, which can each be broken down into those 90-degree twists, and because each 90-degree twist involves those cycles of 2c and 3c pieces, the 2c and 3c pieces share the same parity, meaning the 2c pieces are in an odd permutation if and only if the 3c pieces are in an odd permutation.
Theorem 2: No odd permutations of \(m\)-coloured pieces are possible on an \(s^n\) cube for \(n \ge 4\), \(1 \le m \le n\), and \(s \ge 2\), where \(s\) is even. In other words, every solvable permutation on such a puzzle is composed of even permutations of all piece types.
Proof sketch: Consider a solved \(s^n\) cube. A single 90-degree twist on a single slice of that puzzle involves rotating an \(s^{n-1}\) block of pieces. We split that slice into a 2x2x2 grid of \((s/2)^{n-1}\) pieces, which is well-defined because \(s \ge 2\) is even, and because \((n - 1) \ge 3\). We choose two adjacent octants \(O_1\) and \(O_2\). There is then a plane bisecting those octants. Rotating \(S\) along that plane by a single 90-degree twist results in two 4-cycles of octants. We then decompose that rotation further by considering it as a disjoint sum of 4-cycles of pieces. Each of those 4-cycles can then be associated with a piece in either \(O_1\) or \(O_2\). Because one can also rotate \(O_1\) to \(O_2\) and vice versa, there is a mapping between the pieces in the two octants, and so the 4-cycles can be considered in pairs. Therefore, for all \(1 \le m \le n\), the 4-cycles of the \(m\)-coloured pieces of the rotated slice can be considered in pairs. One 4-cycle is an odd permutation, but an even number of them is an even permutation, so the overall permutation of each \(m\)-coloured piece is even.
Because every solvable permutation can be broken down into a series of valid facet twists, which can each be broken down into those 90-degree twists, and because each 90-degree twist results in an even permutation of all piece types, all solvable permutations on the puzzle are composed of even permutations of all piece types.
Examples
Pseudo-OLL parity cases
By Theorem 2, even if a situation that looks like OLL parity occurs on a higher-dimensional even-layered cube, it can be solved using 3-cycles or other commutators, which are also even permutations. I therefore call those cases pseudo-OLL parity cases.
For example, a common situation on the 4x4x4x4 cube when using a reduction method is a single flipped 2x2x1x1 block of paired 2c pieces (Figure 3). One can solve it using the regular OLL parity algorithm, but one can also solve it using commutators.

Figure 3: A single block of 2c pieces flipped on the 4x4x4x4 in Magic Cube 7D.
Another example of theorem 2 occurs on the 4x4x4x4x4 where a single paired 2x2x1x1x1 block of 3c pieces can be flipped (Figure 4). Using the OLL parity algorithm does not work in this case, because that flips an entire 2c block instead of a 3c block. Using the RKT version of the OLL parity algorithm does not work either, because that introduces an RKT offset, meaning it leaves an entire slice of the puzzle unsolved. Therefore, one needs to use commutators to resolve this situation.
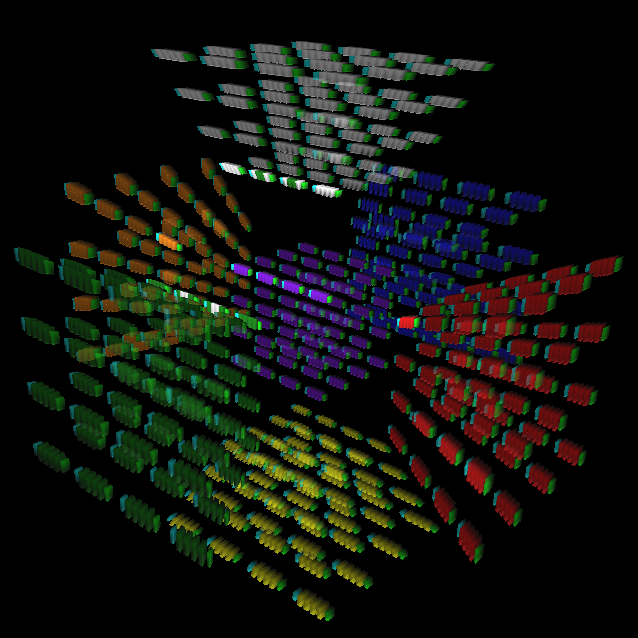
Figure 4: A single block of 3c pieces flipped on the 4x4x4x4x4 in Magic Cube 7D. The program was adjusted to emphasize the area containing the flipped block.
Odd parity on the 2x2x2
Theorem 2 only applies to puzzles above three dimensions. Meanwhile, Theorem 1 explains why a single swap of corner pieces is possible on the 2x2x2 (Figure 5). Because some beginners learn only a single 3-cycle algorithm to help them with corner permutation when solving the 3x3x3, a single swap of corner pieces often confuses them when they attempt to solve the 2x2x2 for the first time.

Figure 5: A single swap of corner (3c) pieces on the 2x2x2 in Twizzle.
Conclusion
OLL parity occurs on even-layered puzzles in three dimensions, such as the 4x4x4, because a single 90-degree slice move results in a single 4-cycle of the edge pieces, which is an odd permutation. On higher-dimensional even-layered puzzles, all permutations are even over all piece types, so OLL parity cannot occur due to the actual parity of the permutation of a certain piece type being odd. It turns out other cases that look like OLL parity can occur, but they can all be fixed using commutators. Meanwhile, odd permutations of 2-coloured and 3-coloured pieces can still occur on higher-dimensional \(3^n\) puzzles, as well as the 2x2x2.
Go back to Articles